| Главная » Статьи » Учебники » Эконометрика |
В ходе статистического изучения функциональных связей достаточно часто возникает задача аппроксимации результатов наблюдений аналитической зависимостью. Один из подходов к ее решению основывается на теореме Вейерштрасса, гласящей, что любая непрерывная функция с точностью до сколь угодно малого δ> 0 может быть аппроксимирована многочленом. Например:
Для построения подобных полиномиальных моделей наряду с другими методами используют регрессионный анализ. Выбор вида (степени) многочлена при этом предоставлен интуиции исследователя. Из рассмотренной задачи непосредственно следуют две другие задачи: 1) определение коэффициентов βs выбранного многочлена и статистическая оценка их значимости; 2) проверка (оценка) адекватности выбранной математической модели. Решение перечисленных задач возможно лишь при выполнении ряда допущений, или предпосылок, регрессионного анализа: 1. Результаты измерений (y1, y2, ...,yn) - попарно независимые случайные величины, т.е. корреляционный момент связи Куiуj =0, i,j = 1, 2, ..., n. 2. Случайные величины (y1, y2, ...,yn) имеют нормальное распределение (при нормальном распределении отсутствие корреляции свидетельствует о независимости случайных величин). 3. Дисперсия воспроизводимости σy2, однородна по всему факторному пространству. 4. Управляемые переменные (факторы) являются неслучайными переменами, т.е. 5. Управляемые переменные линейно независимы, т.е. ни одна из переменных не может быть представлена в виде линейных комбинаций других. 6. В выражении Ү =η(x)+ε(x), где х (х1, х2,..., хn), предполагается М[ε(х)]=0, т.е. M[Y]=η(х). 7. Функция отклика (уравнение регрессии) линейна по параметрам, т.е. Наиболее распространенными примерами линейных по параметрам функций являются полиномы различных степеней. | |
| Просмотров: 2639 | | |
| Всего комментариев: 0 | |

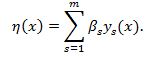
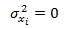 или
или