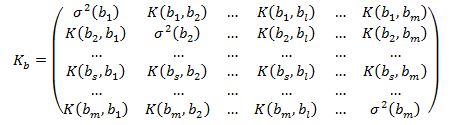| Главная » Статьи » Учебники » Эконометрика |
Полученное по опытным данным уравнение регрессии без статистического анализа остается лишь статистической гипотезой и, как всякая гипотеза, требует проверки. Целью статистического анализа уравнения регрессии является: 1) проверка выполнимости некоторых предпосылок регрессионного анализа, в частности проверка однородности дисперсии воспроизводимости, проверка независимости результатов эксперимента и т.д.; 2) установление степени адекватности регрессионной модели, т.е. степени соответствия функции отклика опытным данным; 3) оценка эффектов факторов и их взаимодействий, т.е. оценка вкладов факторов в величину отклика; 4) оценка способности уравнения регрессии предсказывать значение функции отклика при различных сочетаниях уровней факторов, т.е. в тех точках факторного пространства, в которых опыты не ставились. Центральным этапом статистического анализа является проверка адекватности регрессионной модели. Только в рамках адекватной модели можно делать определенные выводы и принимать обоснованные решения. Неадекватная модель практической полезностью почти не обладает. Для проверки адекватности уравнения регрессии необходимо, чтобы число степеней свободы было больше нуля. В регрессионном анализе число степеней свободы h определяется как разность между числом опытов N, по которым оценивают параметры регрессии, и числом параметров m. Таким образом, h = N - m Число N может не совпадать с числом точек факторного пространства n, в которых ставились опыты, ибо в одной и той же точке (при одном и том же комплексе условий) может быть поставлено несколько опытов. Следовательно, всегда N >n. При отрицательном числе степеней свободы N< n метод наименьших квадратов не может быть использован. При h=0, т.е. N=m (так называемый насыщенный эксперимент), уравнение регрессии может быть получено, однако статистический анализ этого уравнения нельзя провести, так как для проверки адекватности модели не остается степеней свободы. После установления адекватности модели оценивают значимость коэффициентов регрессии. Факторы с незначимыми эффектами после дополнительной проверки могут быть отсеяны. При статистическом анализе выявляют также корреляцию оценок коэффициентов регрессии. Для этого приходится находить ковариационную матрицу оценок коэффициентов. На основе этой матрицы можно достаточно полно исследовать точность предсказания отклика по уравнению регрессии.
В регрессионном анализе ковариационная матрица оценок коэффициентов регрессии играет важную роль. Определитель этой матрицы называют обобщенной дисперсией оценок коэффициентов регрессии. По величине обобщенной дисперсии можно судить о качестве эксперимента. При нормальном распределении результатов эксперимента и использовании метода наименьших квадратов оценки коэффициентов bs также подчиняются нормальному распределению. В общем случае при m коэффициентах регрессии можно построить m-мерный эллипсоид рассеивания. Объем этого эллипсоида характеризуется определителем ковариационной матрицы оценок коэффициентов регрессии, т.е. обобщенной дисперсией оценок коэффициентов. Понятно, что эксперимент, которому соответствует эллипсоид рассеивания с меньшим объемом, при прочих равных условиях лучше эксперимента с большим объемом эллипсоида рассеивания. При увеличении числа опытов, по результатам которых строится уравнение регрессии, объем эллипсоида сокращается. Однако, оставляя постоянным число опытов, можно добиться уменьшения объема эллипсоида рассеивания оценок рациональным распределением экстремальных точек в факторном пространстве (если это возможно). Точность регрессионной модели характеризуется дисперсией предсказанного по уравнению регрессии отклика. Следует отметить, что оценивание точности регрессионной модели, как и другие перечисленные выше процедуры статистического анализа уравнения регрессии, оправданны лишь в случае, если выполняются основные предпосылки регрессионного анализа. Одной из таких предпосылок является допущение об однородности дисперсии воспроизводимости наблюдаемой переменной. | |
| Просмотров: 2731 | | |
| Всего комментариев: 0 | |