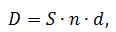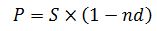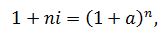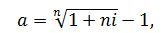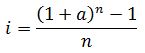| Главная » Статьи » Учебники » Финансовые вычисления |
Принцип неравноценности денег во времени получен эмпирическим путем. Известно, что рубль сегодняшний стоит дороже рубля будущего. Причем приращение превышает инфляционные потери. Этот принцип является основой любого бизнеса. Если в настоящее время 1 руб. можно инвестировать под заданный процент на заданный период, то через этот период инвестор получит 1 руб. плюс процент. Проценты – это абсолютная величина дохода от предоставления денег в долг в любой его форме. Наращенная сумма ссуды – это первоначальная сумма плюс начисленные к концу срока ссуды проценты:
где S – наращенная сумма ссуды; Процентная ставка является также измерителем степени доходности любой финансовой операции. В этом случае процентная ставка называется доходностью. Простая процентная ставка наращения – это ставка, при которой база начисления всегда остается постоянной. Проценты I за весь срок ссуды вычисляются по формуле:
где n – срок ссуды в годах; i – простая годовая ставка наращения. Подставив выражение для процентов (2) в соотношение (1), получим формулу наращенной суммы с использованием простых процентов:
Множитель q = (1+ni) называется множителем наращения простых процентов. Срок ссуды рассчитывается по формуле:
где t – число дней ссуды; K – временная база (число дней в году). В зависимости от принятой методики используют два типа временных баз: К = 360 – обыкновенные проценты; К = 365 (366) – точные проценты. Сложная процентная ставка наращения – это ставка, при которой база начисления является переменной, т. е. проценты начисляются на проценты.
При дисконтировании вычисляют современную стоимость будущего платежа. Другими словами, находят современное Р будущего платежа S, который будет выдан через срок n по ставке дисконтирования i. Для простых процентов:
Для сложных процентов:
Множители
Разность D = S – P называется дисконтом с суммы S. Учетными ставками называются ставки, используемые при учете векселей. Банк может учесть вексель до наступления срока платежа с дисконтом, т. е. купить его у владельца по цене, которая меньше номинала S, указанного в векселе. Размер дисконта при учете по простой учетной ставке определяется по формуле:
где d – простая учетная ставка; n – срок от момента учета до момента погашения. Сумма, выплачиваемая владельцу векселя при учете по простой процентной ставке:
Множитель (1 – nd) называется дисконтным множителем. Эквивалентными процентными ставками называются любые две ставки, которые при замене одной на другую приводят к одинаковым финансовым результатам, т. е. отношения сторон не изменяются в рамках одной финансовой операции. Определим соотношения эквивалентности между простой и сложной процентными ставками наращения. При этом полагаем, что начальные и наращенные суммы при применении рассматриваемых ставок одинаковы. Поэтому для решения поставленной задачи приравниваем множители наращения друг к другу. В результате получим:
где i – простая процентная ставка; a – сложная процентная ставка; n – срок операции в годах. Решив уравнение относительно a и i, получим, соответственно, сложную процентную ставку наращения:
простую процентную ставку наращения:
| |||||||||||
| Просмотров: 2478 | | | |||||||||||
| Всего комментариев: 0 | |

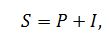
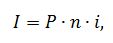
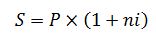
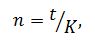
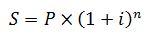
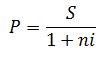 .
.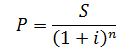 .
.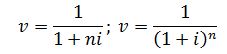 называются дисконтными множителями.
называются дисконтными множителями.