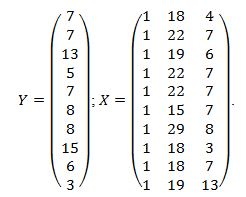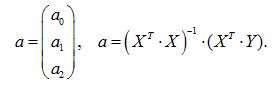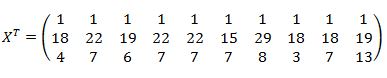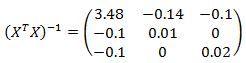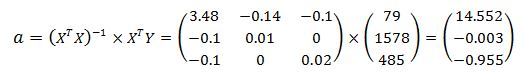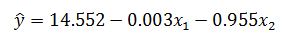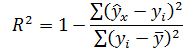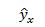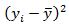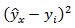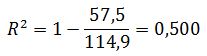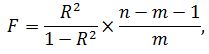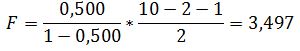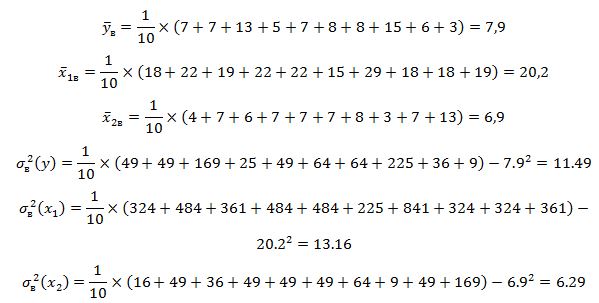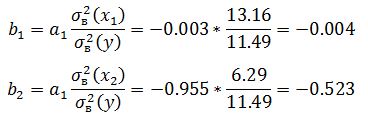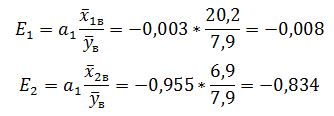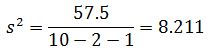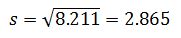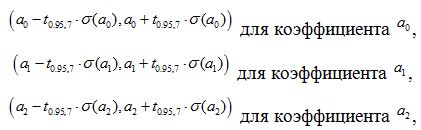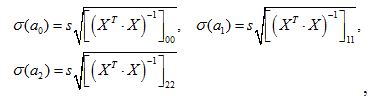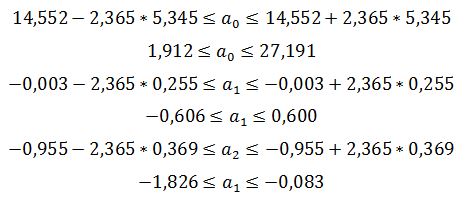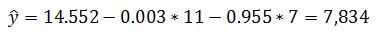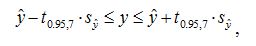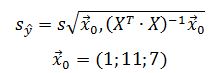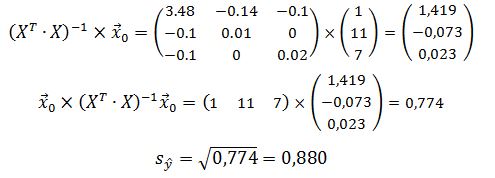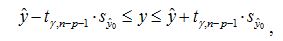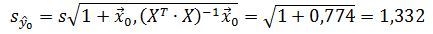Задача

Имеются следующие данные о выработке литья на одного рабочего x₁ (т), браке литья x₂ (%) и себестоимости 1 т литья (т. руб.) по 10 литейным заводам:

В предположениях классической линейной модели требуется:

1. найти множественный коэффициент детерминации и пояснить его смысл;
2. найти уравнение Y_x = a₀ + a₁x₁ + a₂x₂  множественной регрессии Y_x на x₁, x₂, и оценить значимость этого уравнения и его коэффициентов на уровне a=0.05;
3. сравнить раздельное влияние на зависимую переменную каждой из объясняющих переменных, используя стандартизированные коэффициенты регрессии и коэффициенты эластичности;
4. найти 95 %-ные доверительные интервалы для коэффициентов регрессии, а также доверительные интервалы для среднего и индивидуального показателей значения себестоимости 1 т литья в цехах, в которых выработка литья на 1 рабочего составляет 11 т, а брак литья – 7%.

Решение

1. Оценка параметров множественной линейной регрессии

Расчет параметров линейной множественной регрессии проводится в матричной форме:

Тогда:

Найдем последовательно матрицу  и вектор (X^TX)^-1. Имеем X^TY

Теперь вычислим обратную матрицу (X^TX)^-1:

Остается перемножить матрицу (X^TX)^-1 и вектор X^TY:

Уравнение регрессии имеет вид:

Полученное уравнение означает, что при увеличении выработки одного рабочего на 1 т себестоимость одной тонны литья снизится в среднем на 0,003 тыс. руб. При увеличении брака на 1% себестоимость 1 тонны литья снизится в среднем на 0,955 тыс. руб.

Очевидно, что фактор x₂ оказывает гораздо большее влияние на результативный признак, чем фактор x₁.

2. Расчет множественного коэффициента детерминации

Множественный коэффициент детерминации определяется по формуле:

Вспомогательные расчеты для оценки коэффициента детерминации приведены в таблице.

Расчет множественного коэффициента детерминации

Множественный коэффициент детерминации равен:

Полученное значение коэффициента детерминации означает, что 50% вариации себестоимости одной тонны литья объясняется построенным регрессионным уравнением, а 50% – влиянием прочих факторов.

3. Оценка значимости уравнения  и его коэффициентов

Оценка значимости уравнения в целом осуществляется с помощью F-критерием Фишера:

где:   n – число наблюдений;
m – число параметров при переменных x.

F-критерий Фишера равен:

Табличное значение F-критерия для уровня значимости 0,05 и числа степеней свободы k₁=m=2 и k₂=n–m–1=7 равно 4,737.

Поскольку расчетное значение F-критерия ниже табличного, принимается нулевая гипотеза о том, что коэффициент детерминации равен нулю, т.е. построенное уравнение регрессии статистически незначимо.

Найдем точечные оценки для всех имеющихся переменных:

Найдем стандартизированные регрессии и коэффициенты эластичности для каждой из объясняющих переменных. Имеем:

Так как стандартизированный коэффициент регрессии для второго фактора больше, то он оказывает большее влияние на результативный признак. Стандартизированный коэффициент регрессии при переменной x₁ близок к нулю, что говорит о том, что влияние фактора на себестоимость литья несущественно.

Рассчитаем коэффициенты эластичности:

Это означает, что при изменении фактора x₁ на 1% результативный признак изменится на 0,008% в противоположном направлении. При изменении фактора x₂ на 1% результативный признак изменится на 0,834%.

Таким образом, влияние фактора «Процент брака» более существенно, чем переменной «Выработка литья на одного рабочего».

4. Определение доверительных интервалов для коэффициентов регрессии

Точечная оценка остаточной дисперсии:

Остаточное среднеквадратическое отклонение:

Доверительные интервалы с доверительной вероятностью 0.95 для коэффициентов регрессии имеют вид

где

элементы, стоящие на диагонали матрицы (X^TX)^-1. Матрица (X^TX)^-1 была ранее найдена в явном виде, поэтому

Табличное значение критерия Стьюдента для числа степеней свободы 7 и уровня значимости 0,05 равно 2,365. Доверительные интервалы для коэффициентов регрессии равны:

Расчеты показывают, что доверительный интервал для параметра a₁ включает в себя 0, т.е. с вероятностью 95% коэффициент регрессии а₁ равен нулю. Это означает, что переменная x₁ не влияет на результативный фактор.

Рассчитаем прогнозное значение себестоимости одной тонны литья, если выработка одного рабочего составляет 11 т, а процент брака – 7%:

Формула для доверительного интервала для средних значений переменной имеет вид

где:

Получаем:

Доверительный интервал для среднего значения результативного признака равен:

Y ϵ (7,834 - 2,365*0,880; 7,834 + 2,365*0,880) = (5,754; 9,915)

Вывод: с вероятностью 95% средняя себестоимость тонны литья при выработке одного рабочего 11 т и проценте брака 7% находится в интервале от 5,754 до 9,915 тыс. руб.

Для индивидуальных значений переменной Y соответствующий доверительный интервал имеет вид:

где:

Откуда:

Y ϵ (7,834 - 2,365*1.332; 7,834 + 2,365*1.332) = (4.685; 10.984)

Вывод: индивидуальное значение признака при выработке 11 т и уровне брака 7% с вероятностью 95% находится в пределах от 4,685 до 10,984 тыс. руб.