| Главная » Статьи » Решение задач » Задачи по статистике |
ЗаданиеРассчитать среднюю арифметическую, моду и медиану числа торговых точек (в дискретном ряду распределения).
Решение Для расчета среднего числа торговых точек, приходящегося на одно хозяйство, используется формула средней арифметической взвешенной:
где: xi – значение признака; По данным таблицы определим значение средней арифметической:
Мода (Мо) представляет собой значение изучаемого признака, повторяющегося с наибольшей частотой. По данным таблицы 1.2 видно, что наибольшей частотой (10 хозяйств) обладает значение х=5. Следовательно, мода дискретного ряда равна: Mo = 5 Медианой (Ме) называется значение признака, приходящегося на середину ранжированной (упорядоченной) совокупности. Для определения медианного значения признака необходимо определить номер медианной единицы ряда по следующей зависимости:
где n – объем совокупности. Для дискретного вариационного ряда номер медианной единицы равен:
т.е. середина ряда распределения находится между 15-м и 16-м хозяйствами. Необходимо определить, к какой группе относятся хозяйства с этими номерами. Это можно определить, рассчитав кумулятивные частоты. Кумулятивная частота для первой группы равна 2, для второй – 7 (2+5), для третьей – 12 (2+5+5), для четвертой – 22 (2+5+5+10). Следовательно, середина ряда распределения приходится на четвертую группу хозяйств – с числом торговых точек равным 5: Me=5 | |||||||||||||||||||||||||
| Просмотров: 1582 | | | |||||||||||||||||||||||||
| Всего комментариев: 0 | |

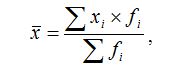 ,
,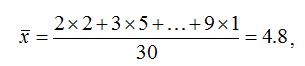 ,
,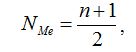 ,
,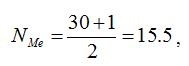 ,
,