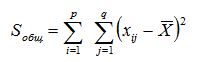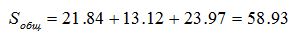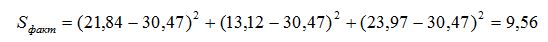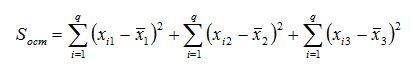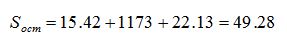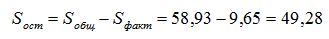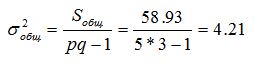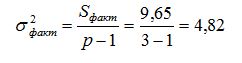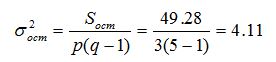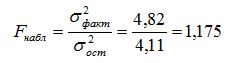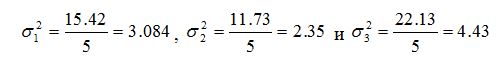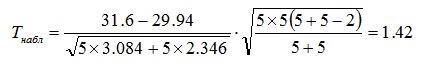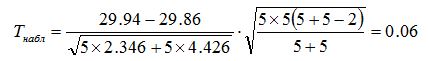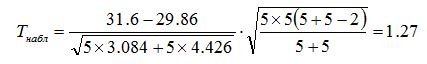| Главная » Статьи » Решение задач » Задачи по статистике |
Задача
Исходные данные для дисперсионного анализа
Решение
Общее среднее по результатам испытаний рассчитывается по данным таблицы: Расчет групповых средних
Общее среднее равно:
Групповые средние:
Общая сумма квадратов отклонений наблюдаемых значений от общей средней
и рассчитывается по таблице:
Общая сумма квадратов отклонений наблюдаемых значений от общей средней равна:
Факторная сумма квадратов групповых отклонений от общей средней:
Остаточная сумма квадратов отклонений наблюдаемых значений группы от своей групповой средней, определяется по формуле:
Квадраты отклонений значений от групповых средних рассчитаны в таблице:
Остаточная сумма квадратов отклонений наблюдаемых значений группы от своей групповой средней равна:
Остаточная сумма квадратов должна быть равна разнице между общей суммой и факторной суммой квадратов:
Разделив суммы квадратов отклонений на соответствующее число степеней свободы, получим общую, факторную и остаточную дисперсии. Общая дисперсия:
Факторная дисперсия:
Остаточная дисперсия:
Сравним факторную и остаточную дисперсию по критерию Фишера-Снедекора, для чего найдем наблюдаемое значение критерия:
Учитывая, что число степеней свободы числителя k1=2, а знаменателя k2=12, уровень значимости 0,05, находим критическую точку: Fкр(0,05; 2; 12) = 3,88 Наблюдаемое значение меньше критического, следовательно гипотеза о равенстве средних подтвердилась. Для попарного сравнения средних воспользуемся критерием Стьюдента. На основе таблицы 5.4 рассчитаем групповые дисперсии:
Рассчитаем наблюдаемый критерий Стьюдента для:
Критическое значение критерия Стьюдента для уровня значимости 0,05 и числа степеней свободы 5+5-2=8 составляет tкр=2,31. Поскольку все рассчитанные наблюдаемые значения критерия Стьюдента меньше критического, гипотеза о равенстве средних подтверждается. Гипотеза о равенстве средних подтвердилась по результатам дисперсионного анализа, следовательно выборки зависимы, т.е. входят в общую генеральную совокупность. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Просмотров: 5330 | | | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Всего комментариев: 0 | |

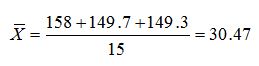
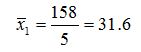
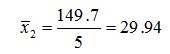
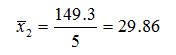
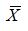 определяется по формуле:
определяется по формуле: