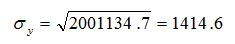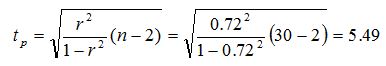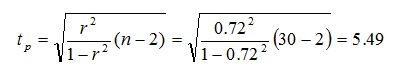Главная » Статьи » Решение задач » Задачи по статистике
Задача №22. Корреляционный анализ

Задача 

Провести корреляционный анализ зависимости выручки от числа торговых точек.

Исходные данные для корреляционного анализа

№

Число торговых точек (X)

Выручка (Y)

XY

 
  1.  

2

1598

3196

7,84

2291792,3

 
  1.  

5

2644

13220

0,04

218899,2

 
  1.  

4

2197

8788

0,64

836981,0

 
  1.  

5

1959

9795

0,04

1329101,6

 
  1.  

3

1052

3156

3,24

4243050,7

 
  1.  

3

1922

5766

3,24

1415782,7

 
  1.  

5

2385

11925

0,04

528335,2

 
  1.  

5

2581

12905

0,04

281819,4

 
  1.  

5

3105

15525

0,04

47,2

 
  1.  

4

3896

15584

0,64

614865,1

 
  1.  

4

1510

6040

0,64

2565976,8

 
  1.  

2

1880

3760

7,84

1517495,5

 
  1.  

5

3620

18100

0,04

258199,5

 
  1.  

6

5002

30012

1,44

3572604,0

 
  1.  

5

2819

14095

0,04

85770,9

 
  1.  

4

4076

16304

0,64

929553,1

 
  1.  

6

1869

11214

1,44

1544717,6

 
  1.  

3

3524

10572

3,24

169853,9

 
  1.  

6

3925

23550

1,44

661185,8

 
  1.  

4

1998

7992

0,64

1240699,0

 
  1.  

3

2606

7818

3,24

255901,1

 
  1.  

5

2353

11765

0,04

575878,6

 
  1.  

3

2981

8943

3,24

17126,1

 
  1.  

7

4471

31297

4,84

1847243,4

 
  1.  

6

2308

13848

1,44

646201,6

 
  1.  

5

4563

22815

0,04

2105788,0

 
  1.  

7

4306

30142

4,84

1425954,4

 
  1.  

5

2541

12705

0,04

325888,8

 
  1.  

8

6184

49472

10,24

9438003,2

 
  1.  

9

7481

67329

17,64

19089326,1

 

Итого:

144

93356

497633

78,8

60034041,5

 

Решение

Линейный коэффициент корреляции характеризует тесноту и направление связи между двумя коррелируемыми признаками в случае наличия между ними линейной зависимости:

Среднее число торговых точек равно:

Средняя выручка:

Средний показатель XY:

 

Дисперсия количества торговых точек:

,

а среднеквадратическое отклонение:

Дисперсия выручки:

,

среднеквадратическое отклонение:

Коэффициент корреляции равен:

Значимость линейного коэффициента корреляции проверяется на основе t-критерия Стьюдента. При этом выдвигается и проверяется нулевая гипотеза (Н0) о равенстве коэффициента корреляции нулю [Н0: r=0] При проверке этой гипотезы используется t-статистика.

Если расчетное значение tр >tкр, то гипотеза Н0 отвергается, что свидетельствует о значимости линейного коэффициента корреляции, а следовательно, и о статистической существенности зависимости между Х и У.

Критическое значение критерия Стьюдента при числе степеней свободы 30-2=28 и уровне значимости 0,05 равно tкр=2,05. Рассчитанное значение показателя больше критического, следовательно, между выручкой и количеством торговых точек есть статистическая зависимость.

Категория: Задачи по статистике | Добавил: Mirka (03.09.2014)
Просмотров: 13176 | Теги: корреляционный анализ, задачи по статистике | Рейтинг: 0.0/0
Всего комментариев: 0
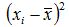
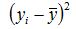
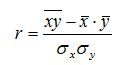
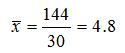
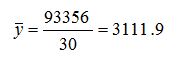
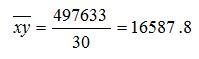
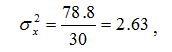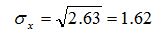
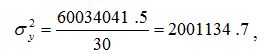Войдите:
avatar