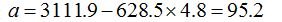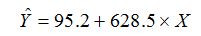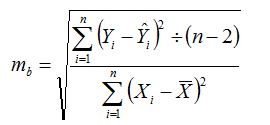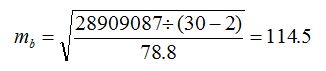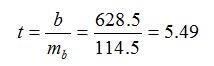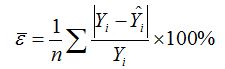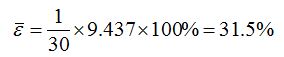| Главная » Статьи » Решение задач » Задачи по статистике |
ЗадачаПровести регрессионный анализ зависимости выручки от числа торговых точек. Таблица 1 Исходные данные
РешениеРегрессионный анализ заключается в определении аналитического выражения связи, в котором изменение одной величины (называемой зависимой или результативным признаком) обусловлено влиянием одной или нескольких независимых величин (факторов), а множество всех прочих факторов, также оказывающих влияние на зависимую величину, принимается за постоянные и средние значения. Парная регрессия характеризует связь между двумя признаками: факторным и результативным. Уравнение регрессии имеет вид: Y = ax + b, где: Y — результативный показатель; Оценка параметров уравнений регрессии (а0, а1, …аn) производится на основе метода наименьших квадратов. Для парной линейной регрессии система нормальных уравнений, полученная на основе метода наименьших квадратов имеет вид:
где n – количество наблюдений; В таблице приведены исходные данные для расчета параметров регрессии. Таблица 2
Система уравнений для расчета параметров регрессии имеет вид:
Для решения системы уравнений удобно преобразовать их. После преобразования получим следующие формулы для расчета параметров регрессии:
Средние величины рассчитаем по таблице:
Дисперсия факторного признака равна:
Отсюда найдем параметры регрессии:
Уравнение регрессии имеет вид:
Подставив в полученное уравнение значения факторного признака из табл. 1, определим расчетное значение результативного показателя (табл.2). Для проверки значимости полученного уравнения рассчитаем среднюю ошибку для коэффициента парной регрессии b:
Расчет средней ошибки для коэффициента b осуществляется по данным табл. 2:
Критерий Стьюдента рассчитывается по формуле:
Критическое значение критерия при уровне значимости 0,01 и числе степеней свободы 30-2=28 составляет 2,763. Полученное значение критерия намного больше табличного, следовательно, гипотезу о незначительности регрессионной связи между показателями можно отклонить. Это означает, что между количеством торговых точек и выручкой существует регрессионная связь. Для надежности полученного уравнения регрессии используют показатель средней ошибки аппроксимации:
По данным таблицы 2 определим среднюю ошибку аппроксимации:
Из расчета видно, что средняя ошибка аппроксимации слишком велика, следовательно полученное уравнение регрессии имеет слишком большую погрешность и не может быть использовано для прогнозирования. Таким образом, из расчетов очевидно, что между количеством торговых точек и выручкой существует зависимость. Однако модель, построенная в результате регрессионного анализа имеет слишком высокую погрешность и для прогнозирования выручки использована быть не может.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Просмотров: 10301 | | | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Всего комментариев: 0 | |

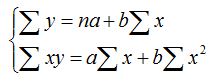
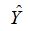
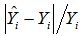
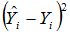
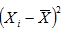
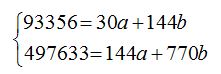
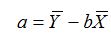 и
и 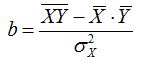
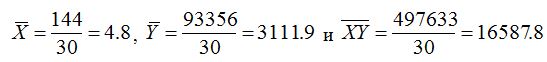
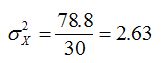
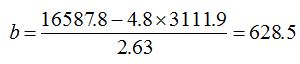 и
и