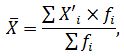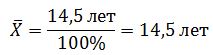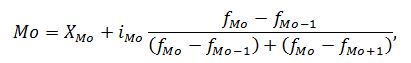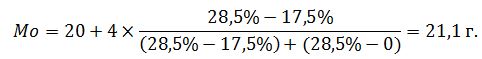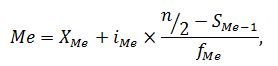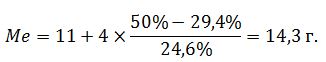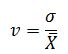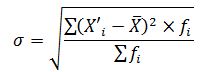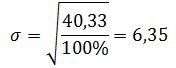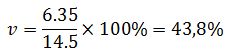Задача

Известны следующие данные о возрастной структуре производственного оборудования по промышленности:

Определите:

1. средний возраст производственного оборудования;
2. модальный и медианный возраст производственного оборудования;
3. применяя коэффициент вариации, сформулируйте вывод о возможности использования рассчитанных показателей в качестве средней величины.

Решение

Для расчета среднего возраста оборудования будет использована формула средней арифметической взвешенной. Но поскольку значения представлены в виде интервального ряда, в качестве значений X_i необходимо использовать середину интервала:

где:    X’_i – середина интервала;
f_i – частота интервала.

Средний возраст оборудования равен:

Мода – это значение, имеющее наибольшую частоту в вариационном ряду. В данном случае модальным интервалом является интервал «Более 20 лет», имеющий частоту 28,5%.

Для расчета конкретного значения моды используют формулу:

где:   X_Mo  – нижняя граница модального интервала;
i_Mo – величина модального интервала;
f_Mo, f_Mo-1, f_Mo+1  – частоты в модальном, предыдущем и следующем за модальным интервалах соответственно.

Модальное значение возраста оборудования равно:

Медиана – это вариант, который находится в середине вариационного ряда. Медиана делит ряд на две равные (по числу единиц) части – со значениями признака меньше медианы и со значениями признака больше медианы. В нашем случае медианным является интервал, которому принадлежит накопленная частота 50%. Это интервал «11-15 лет». Для расчета точечного значения медианы используют формулу:

где:  X_Me   – нижняя граница медианного интервала;
i_Me – величина медианного интервала;
n/2 – половина от общего числа наблюдений;
S_Me-1 – накопленная частота предыдущего интервала;
f_Me – частота медианного интервала.

Медиана равна:

Коэффициент вариации определяется как отношение средне­квадратического отклонения (σ) к среднему значению признака:

Среднеквадратическое отклонение определяется по формуле:

Среднеквадратическое отклонение для данного вариационного ряда равно:

Коэффициент вариации равен:

Выводы:   из расчетов видно, что средний возраст оборудования составил 14,5 лет, модальное значение – 21,1 г., медиана – 14,3 г. Среднее значение, мода и медиана находятся в разных интервалах, что свидетельствует о неоднородности и несимметричности распределения. Кроме того, значение коэффициента вариации больше 33% (43,8%) говорит о количественной неоднородности распределения. Следовательно, рассчитанные показатели не могут быть использованы в качестве средней величины.