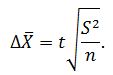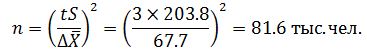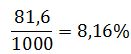| Главная » Статьи » Решение задач » Задачи по статистике |
Задача 15Центром экономических исследований при органах регионального управления проведено выборочное наблюдение с целью изучения расходов населения на коммунальные услуги. В результате двухпроцентного обследования получены следующие данные:
Определите:
РешениеДля определения средней величины доходов населения необходимо определить середину интервала и умножить ее на частоту данного интервала.
Средняя величина расходов населения на коммунальные услуги равна:
Доля населения региона, у которых расходы на коммунальные услуги находятся в пределах 600-1000 руб.:
Предельная ошибка для среднего значения определяется по формуле:
где: t – нормированное отклонение – «коэффициент доверия», зависящий от вероятности, с которой гарантируется предельная ошибка выборки (для вероятности 0,954 – 2, для 0,997 – 3); Дисперсия выборки равна:
Предельная ошибка выборки для среднего значения равна:
Следовательно, доверительный интервал для среднего значения:
Предельная ошибка выборки для доли определяется следующим образом:
где: w – выборочная доля. Предельная ошибка выборки для доли населения, у которых расходы на коммунальные услуги находятся в пределах 600-1000 руб.:
Доверительный интервал для доли:
Необходимую численность выборки, чтобы уменьшить ее ошибку в два раза, можно определить из формулы предельной ошибки выборки для средней величины (множитель
Желаемая предельная ошибка составляет 67,7 руб. (135,3/2). Отсюда объем выборки равен:
Объем генеральной совокупности равен 1000 тыс. чел. (20 тыс./0,02), следовательно новый объем выборки составит:
Выводы: средние расходы населения на коммунальные услуги, рассчитанные на основе 2%-ной выборки, равны 822 руб./чел., а доля населения, расходы которых на коммунальные услуги составляют от 600 до 1000 руб./чел. – 65% от общей численности. Для распространения полученных результатов на генеральную совокупность были рассчитаны предельные ошибки выборки и получены доверительные интервалы: для среднего – , для доли населения – . Чтобы уменьшить ошибку выборки в два раза, объем выборки необходимо увеличить до 81,6 тыс. чел. или 8,16% от генеральной совокупности. | ||||||||||||||||||||||||||||||||||||||||||||||||||
| Просмотров: 6214 | | | ||||||||||||||||||||||||||||||||||||||||||||||||||
| Всего комментариев: 0 | |

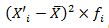
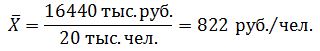
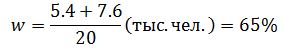
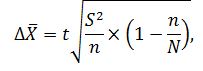
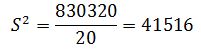
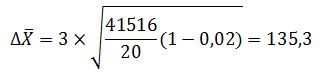
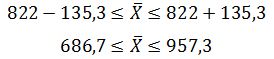
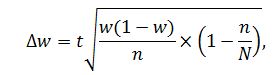
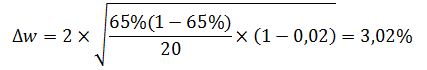
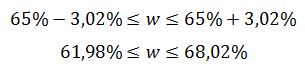
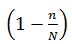 для простоты расчетов отбросим):
для простоты расчетов отбросим):