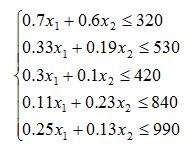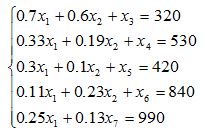| Главная » Статьи » Решение задач » Задачи по математическим методам в экономике |
ЗаданиеПредприятие выпускает торты двух видов. Требуется определить оптимальную структуру товарооборота, обеспечивающую предприятию максимальную прибыль графическим и симплекс методами, если известны следующие данные: М – мука, кг С – сахар, кг О – орехи, кг. УМ – упаковочный материал, м2 В – времени, чел-час. Таблица 1
Решение задачи симплексным методомОбозначим: x1 – объём производства продукта А; Очевидно, что x1 ≥ 0, x2 ≥ 0. Исходя из ограничений на сырье запишем неравенство:
Целевая функция – это прибыль от реализации всей продукции: Z = 24x1 + 48x2 → max Требуется найти x1 и x2 так чтобы они удовлетворяли системе ограничений и прибыль Z была бы максимальной. Запишем эту задачу в форме основной задачи линейного программирования. Для этого перейдем от ограничений-неравенств к ограничениям-равенствам. Введем пять дополнительных переменных, в результате чего ограничения запишутся в виде системы уравнений:
Эти дополнительные переменные по экономическому смыслу означают не используемое при данном плане производства сырье того или иного вида. Составляем симплексную таблицу для первой итерации (табл. 1). Таблица 2
Наибольшее по модулю отрицательное число – -48, следовательно столбец Р2 включаем в базис. Для определения строки, исключаемой из базиса, столбец Р0 необходимо разделить на выбранный столбец Р2. Результат деления приведен в последнем столбце таблицы. Выбираем наименьший результат деления – 533,3. Следовательно, строка Р3 должна быть исключена из базиса. Столбец вектора Р2 и первая строка являются направляющими, а элемент, находящийся на их пересечении, называется разрешающим элементом. Составляем таблицу для второй итерации (табл. 2). Таблица 3
Сначала заполняем строку вектора, вновь введенного в базис, т.е. первую строку. Элементы этой строки находятся делением соответствующих элементов табл. 1 на разрешающий элемент (т.е. 0,6). При этом в столбце Сб записываем коэффициент С2= 48, стоящий в столбце вводимого в базис вектора Р2. Затем заполняем элементы столбцов для векторов, входящих в новый базис. В этих столбцах на пересечении строк и столбцов одноименных векторов проставляем единицы, а все остальные элементы полагаем равными нулю. Для определения остальных элементов табл. 2 применяем правило треугольника. Для вычисления какого-нибудь из этих элементов находят три числа: 1) число, стоящее в исходной симплекс-таблице на месте искомого элемента новой симплекс-таблицы; 2) число, стоящее в исходной симплекс-таблице на пересечении строки, в которой находится искомый элемент новой симплекс-таблицы, и столбца, соответствующего вектору, вводимому в базис; 3) число, стоящее в новой симплекс-таблице на пересечении столбца, в котором стоит искомый элемент, и строки вновь вводимого в базис вектора. Эти три числа образуют своеобразный треугольник, две вершины которого соответствуют числам, находящимся в исходной симплекс-таблице, а третья – числу, находящемуся в новой симплекс-таблице. Для определения искомого элемента новой симплекс-таблицы из первого числа вычитают произведение второго и третьего. Например, элемент, находящийся на пересечении столбца Р0 и второй строки, равен: 530 - 0.19*533.3 = 428.7 Третий элемент столбца Р0 равен: 520 - 0.10*533.3 = 366.7 Аналогично находятся остальные элементы таблицы. По окончании расчетов получаем новый опорный план: X = (0; 533.3; 0.428.7; 717.3; 920.7). При данном плане производства изготовляется 533,3 тортов второго вида, мука используется полностью, остаются неиспользованными: сахар – 428,7 кг, орехи – 366,7 кг, упаковочный материал – 717,3 м2, время – 920,7 чел.-часов. Стоимость продукции составит: 533.3*48 = 25600 д.е. Поскольку отрицательных элементов в симплекс-таблице нет, данный план является оптимальным. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Просмотров: 3334 | | | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Всего комментариев: 0 | |