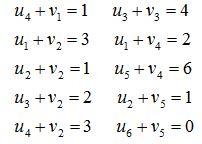| Главная » Статьи » Решение задач » Задачи по математическим методам в экономике |
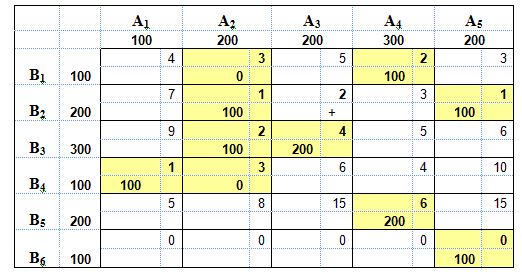
ЗаданиеНа складах а1, а2, а3, а4 и а5 имеются запасы продукции в соответствующих количествах. Найти такой вариант поставки продукции от поставщиков в торговые точки в1, в2, в3, в4 и в5 соответственно, чтобы сумма затрат на перевозку (сij) была минимальна. Для решения использовать метод потенциалов (опорное решение определить методом минимальной стоимости). Таблица 1
Решение задачиРешение транспортной задачи начинается с определения опорного плана. Этот план может быть найден методом северо-западного угла, методом минимального элемента и методом Вогеля. Определим опорный план методом минимального элемента (табл. 2). Сумма запасов составляет 1000, а сумма потребностей – 900, т.е. запасы превышают потребности на 100 ед. Чтобы потребности соответствовали запасам, добавим еще один пункт перевозок с тарифом, равным 0. Таблица 2
Минимальный тариф, равный 0, находится в последней строке таблицы, т.е. можно заполнить любую клетку из этой строки. Например, x65=100, запишем это значение в соответствующую клетку. Строку В6 исключим из рассмотрения, а запасы в столбе А5 составят 100 (200–100). Минимальный тариф по столбцу А5 равен 1. Следовательно, х25=100, столбец А5 исключаем из рассмотрения, а потребности по строке В2=100. Минимальный тариф во второй строке также равен 1 (клетка х22). Следовательно, х22=100, строка В2 исключена из дальнейших расчетов, запасы по столбцу А2 составят 100. Минимальный тариф во втором столбце равен 2. Заполняем клетку х32=100, столбец А2 исключаем из расчетов, потребности по строке В3=200 (300–100). Минимальный тариф по строке В3 равен 4 (клетка х33). Следовательно, х33=200, столбец А3 и строка В3 исключены из расчетов. Теперь минимальный тариф по таблице составляет 1 (клетка х41). х41=100, строка В4 и столбец А1 исключаются из расчетов. Незаполненными остаются две клетки: х14=100 и х54=200. Теперь запасы полностью распределены, а потребности удовлетворены. Стоимость перевозок составляет: 2*100 + 1*100 + 1*100 + 2*100 + 4*200 + 1*100 + 6*200 = 2700 д.е. Количество заполненных клеток должно составить n+m-1 (5+6-1=10). В составленном опорном плане лишь 8 заполненных клеток. Следовательно, необходимо заполнить еще две клетки, чтобы план был невырожденным: x42 = 0 и x12 = 0 Дальше решаем по методу потенциалов. Введём потенциалы поставщиков ui и потенциалы потребителей vj . План является оптимальным, если выполняются условия: Для занятых клеток: ui+vj =cij; Для незанятых клеток: ui+vj ≤cij Составим систему уравнений для занятых клеток:
Подставим v1=0, тогда u4=1, v2=2, u1=1, u2=-1, u3=0, u4=1, v3=4, v5=2, u6=-2, v4=1, u5=5. Запишем значения потенциалов в таблицу (табл. 3). Таблица 3 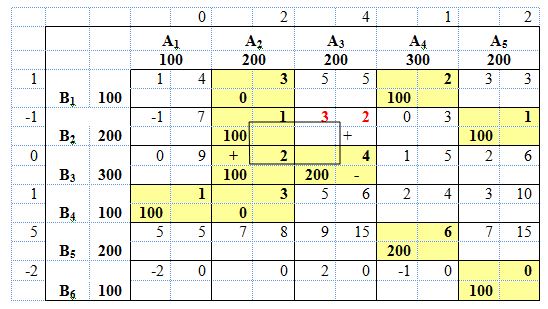 Проверяем условие ui+vj ≤cij для незанятых клеток. Записываем сумму потенциалов в левый верхний угол клетки. В клетке х23 сумма потенциалов (4+(-1)=3) превышает тариф (2). Построим цикл, минимальное значение – 100. Следовательно, в клетку х23 записываем значение 100, в клетках со знаком «–» отнимаем 100 (x33=200–100=100, x22=100–100=0), в клетке со знаком «+» прибавляем 100 (x32=100+100=200).
Результаты записываем в таблицу (табл. 4) и проверяем новый план на оптимальность. Таблица 4
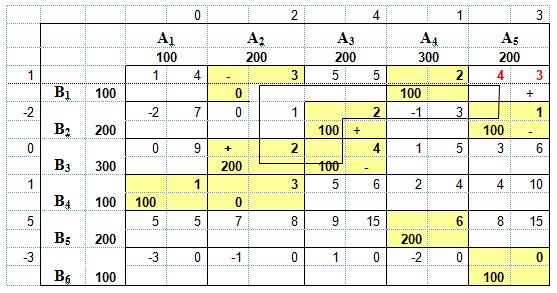 Стоимость перевозок по новому плану составляет: 2*100 + 2*100 + 1*100 + 2*200 + 4*100 + 1*100 + 6*200 = 2600 д.е. Находим потенциалы и проверяем план на оптимальность. В клетке x15 сумма потенциалов превышает тариф перевозок. Построим цикл, минимальное значение в этом цикле составляет 0. Результат запишем в табл. 5. Таблица 5 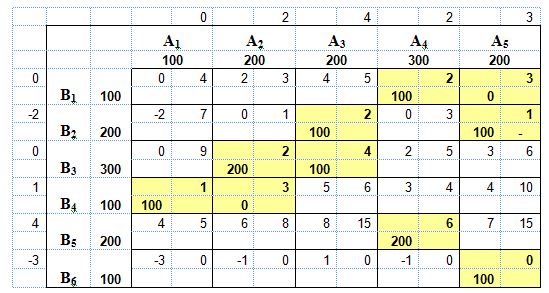 Проверив план на оптимальность, убедились, что сумма потенциалов для незаполненных клеток не превышает тарифов перевозок. Следовательно, найденный план является оптимальным, а стоимость перевозок 2600 д.е. – минимальной стоимостью. | |||||||||||||||||||||||||||||||||||||
| Просмотров: 1427 | | | |||||||||||||||||||||||||||||||||||||
| Всего комментариев: 0 | |