| Главная » Статьи » Решение задач » Задачи по математическим методам в экономике |
ЗаданиеНа складах а1, а2, а3, а4 и а5 имеются запасы продукции в соответствующих количествах. Найти такой вариант поставки продукции от поставщиков в торговые точки в1, в2, в3, в4 и в5 соответственно, чтобы сумма затрат на перевозку (сij) была минимальна. Для решения использовать метод Вогеля. Таблица 1
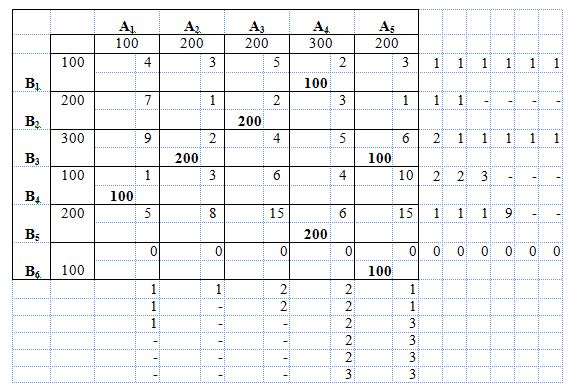
РешениеДля каждой строки и столбца таблицы условий найдем разности между двумя минимальными тарифами, записанными в данной строке или столбце, и поместим их в соответствующем дополнительном столбце или дополнительной строке табл. 2. Например, в строке В1 минимальный тариф равен 2, а следующий за ним – 3. Разность составляет 3–2=1. Записываем это значение в дополнительный столбец. Таблица 2
Наибольшая разница между элементами составляет 2 и соответствует нескольким строкам и столбцам. Например, выберем строку В3. Минимальный тариф в этой строке (2) находится на пересечении со столбцом А2. Заполним эту клетку – х32=200. Запасы пункта А2 распределены, и столбец А2 исключается из расчетов. Потребности пункта В3 составляют 300–200=100. Снова находим разницы между минимальными тарифами, исключив из расчетов столбец А2. Наибольшая разница между тарифами снова равна 2. Выбираем столбец А3, минимальный тариф в этом столбце находится на пересечении со строкой В2 и составляет 2. Заполняем клетку х23=200, столбец А3 и строка В2 исключены из расчетов. Находим разницу между тарифами, наибольшая разница составляет 3 и находится в строке В4. Заполняем клетку х41=100 и исключаем столбец А1 и строку В4 из дальнейших расчетов. Наибольшая разница между тарифами теперь составляет 9 и находится в строке В5. Заполняем клетку х54=200. Строка В5 исключается из расчетов, а запасы в пункте А4 равны 300–200=100. Следующая итерация: максимальная разница между тарифами 3 (столбец А5). Заполняется клетка х65=100, строка В6 исключается из расчетов, запасы в пункте А5 составляют 200–100=100. Следующая итерация: максимальная разница между тарифами 3 (столбец А4). Заполняем клетку х14=100, строка В1 и столбец А4 исключаются из расчетов. Заполняем оставшуюся клетку х35=100. Стоимость перевозок при полученном опорном плане составляет: 2*200 + 2*200 + 6*100 + 1*100 + 6*200 + 0*100 = 2900 д.е. | |||||||||||||||||||||||||||||||||||||
| Просмотров: 1019 | | | |||||||||||||||||||||||||||||||||||||
| Всего комментариев: 0 | |